This is a continuation of two posts: Wicked Problems and Transparent Taming of Wicked Problems
In reviewing practices that appeared to be most effective in designing solutions to wicked problems, Rittel and Webber (1973) recognized that different people perceive the problem (and its solution) differently, that experts sometimes have a too narrow view of the problem and potential solutions, and that wicked problem solving does not proceed in a linear manner. These aspects of solution design have been elucidated by other scholars, and they appear to result in solutions more widely perceived as better than the solutions created when planners follow the methods used to solve tame problems.
Recognizing Diversity
When Rittel and Webber (1973) first defined wicked problems, they concluded that leaders cannot reasonably identify a single solution to a given social problem. They observed “that diverse values are held by different groups of individuals—[so] what satisfies one may be abhorrent to another, [and] what comprise problem-solution for one is problem-generation for another,” and that in this situation, “there is no gain saying which group is right and which should have its end served” (Rittel and Webber 1973, 169). While factors that increase the diversity of the population served by planners complicates the work of designing solutions, imposing a solution or treating a heterogeneous population as homogeneous is not associated with the design of solutions as judged good by diverse subpopulations.
Since the Internet and other media have become available to global audiences, many observers have predicted access to a single collection of media would result in a homogenization of culture, but they appear to have been wrong. The reality that has been emerging is that 21st century media include diverse and niche content, and diverse populations are maintaining strong connections (even when geographically dispersed) over network connections. Well-connected communities are likely to be diverse communities and that poses a challenge to those who design solutions to wicked problems in those populations. Within diverse and connected communities, a solution is also likely to be judged differently by different subpopulations.
When a solution is defined such that one subpopulation finds it satisfactory but another finds it abhorrent; implementation leads to some being winners and others being losers. Game theorists call such situations “zero-sum games.” Many scholars who study wicked problem solving recommend planners attempt to design non-zero sum solutions to wicked problems. In these solutions, all individuals or populations perceive the solutions as advantageous. Those scholars recognize that the win may be disproportional for some, but this outcome is generally regarded as preferential to a zero-sum outcome. Those scholars also concur that the greater the number of choices and the greater diversity offered in the solution(s), the greater the non-zero-sum potential of the solution(s).
Generalized Approach
Buchanan (1991) suggested that planners who focus on a too specialized aspect of a wicked problem are likely to limit the number and diversity of choices in the solution, thus decreasing the potential for non-zero sum outcomes. Buchanan also described an approach to designing solutions to wicked problems that integrates the expertise of specialists from many disciplines, but that make use of a new “liberal arts of technology cultures” (5) that bring more generalized skills and approaches to wicked solution design. According to Buchanan,
without integrative thinking disciplines of understanding, communication and action, there is little hope of sensibly extending knowledge beyond the library or laboratory in order to serve the purpose of enriching human life (6).
For Buchanan, experts’ knowledge and understanding is essential to solving many wicked problems, but that expertise can prevent those individuals from being able to see the problem from other perspectives and that may prevent non-zero-sum solutions from being considered.
The work of designing solutions for wicked problems proceeds from generalizations that can be applied to a wide variety of settings (for educators these generalizations will be elucidated by cognitive and learning scientists) and it focuses on detailing how those generalizations can be instantiated using local resources to meet the particular needs of a local population. Buchanan draws from John Dewey’s educational philosophy to support his suggestion that planners begin designing solutions to wicked problems by developing a working hypothesis that specifies generalizations along with factors from the local setting that will be relevant in creating a particular solution (see figure 5.1). The working hypotheses are based on universal understandings which are indeterminate and, through the design of a solution, are made specific and concrete as a plan for classroom curriculum and instruction is determined. As the working hypothesis and local conditions begin to lead the planner to a solution, the working hypothesis is reassessed and revised. The solution may point to other important generalizations and other relevant conditions defining the problem, and so one tentative solution may point planners to a different final solution.
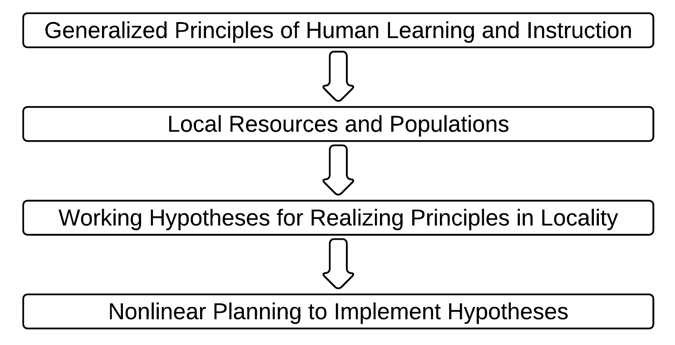
Non-Linear Planning
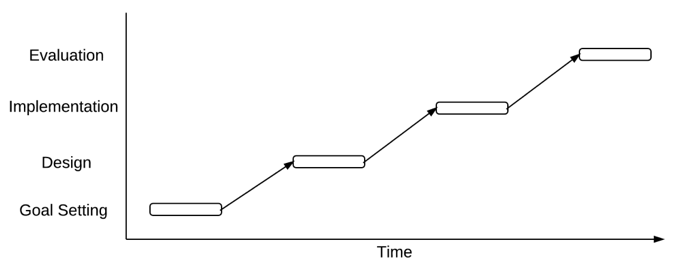
Tame problem solvers typically proceed in a linear fashion beginning with articulating goals, then gathering data, engineering and implementing a solution, and finally to evaluating the solution. Evaluation typically leads the planner to begin the linear process again in an iterative manner; what was learned in the first iteration is used to begin the next iteration. Curriculum and instruction planning that follows this model defines the goals to be met and then proceeds to develop instructional activities to meet those goals. Evaluation leads the educator to refine the plan for the next time the plan is implemented. Evaluation also leads the educator to decide if remediation is necessary, or if students are ready to proceed through the curriculum.
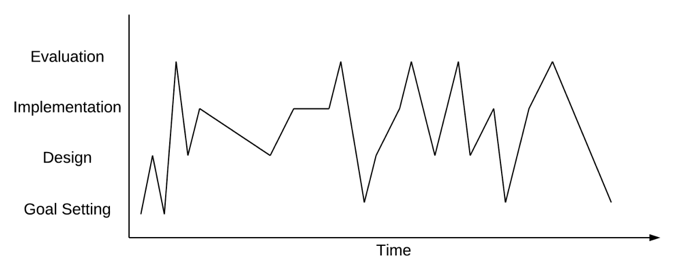
Wicked problem solvers tend to engage in a different process. While they engage in activities that are ostensibly similar to those of tame planners, designers of wicked solutions undertake those activities in no particular order, and they frequently jump between different activities in a manner that the tame planner would perceive as erratic. The differences in how tame and wicked planners differ are illustrated in figures 5.2 and 5.3.
In many ways, the seemingly erratic behavior of those designing solutions to wicked problems is similar to the approach used by hermeneutic researchers. Hermeneutics is a research tradition that originated with scholars who studied religious texts. These researchers sought to elucidate the meanings of sacred texts and they sought to understand the social context in which the texts were composed as a clue to the original meaning of the authors. Over time, the methods of hermeneutic researchers have been used to reconstruct a culture based on the artifacts of the culture. Such methods are frequently applied to analysis of documents, tools, practices, and similar artifacts as data sources.

Hermeneutic researchers fall into the hermeneutic cycle (see figure 5.4) in which an artifact is interpreted in light of the culture and then the culture is reinterpreted in light of the emerging understanding of the artifact. This cycle between the whole of the culture being reconstructed and the parts of the culture embodied in the artifacts continues until the research can justify his or her conclusions. Philosopher Shaun Gallagher (1992) articulates the connection between the hermeneutical approaches to understanding and solving problems and learning and the schools that are designed to support learners:
Things are not disjointed. Parts are parts of a whole. Learning does not consist of stumbling immediately upon an immediate, absolute, and satisfying knowledge of something. Learning is rather searching for understanding within a context” (195).
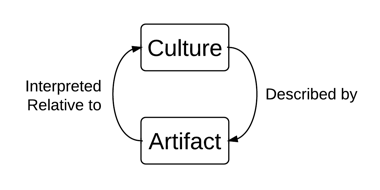
Figure 5.4. The hermeneutic cycle
When planners recognize the wicked nature of their work and they adopt a design process aligned with that proposed by Buchanan (1991) and with the hermeneutic researchers, they will necessarily adopt a Naturalistic stance towards the problems. Naturalistic epistemology generally holds that there are multiple realities and that it is not possible to separate what is known from the knower, and this is generally opposed to positivist epistemology which holds that there is a single reality and that it can be known through controlled and objective observation.
In their seminal book on Naturalistic inquiry, Yvonna Lincoln and Egon Guba (1985) argued that much scientific research is based on a reduction of the problem according to positivist principles, and that those assumptions are increasingly insufficient to describe many problems in the social sciences, including education. Whereas, positivist theory holds that a single reality exists and it can be understood through objective observation, Naturalistic researchers accept that role of the individual in creating and understanding knowledge and meaning. Whereas the positivist holds understanding of and control of causes can lead to predictable effects, the Naturalistic research holds that causes are largely unpredictable and uncontrollable. Also, the positivist holds that observers can make independent observations of situations, but the Naturalistic researcher is an active participant in the situation under study and the researcher is an active participant in data collection.
When adopting a Naturalistic stance towards curriculum and instruction, an educator will recognize that many factors influence decisions and progress and that many sources of data can be used to demonstrate learning. When documenting learning, Naturalistic educators include not only students’ performance on tests and similar ostensibly objective measures, but also students’ experiences and the meaning they make of those experiences. To the Naturalistic educator, there is no difference between a student who can’t solve a problem and one who solves it but for whom it has no meaning. The Naturalistic educator also follows the model of the Naturalistic researcher who undertakes emergent design. The researcher modifies research methods as the study progresses and the educator modifies the lesson as it progresses.
References
Buchanan, Richard. 1992. “Wicked Problems in Design Thinking.” Design Issues 8(2): 5-21. doi:10.2307/1511637.
Gallagher, Shaun. 1992. Hermeneutics and Education. Albany, NY: State University of New York Press.
Lincoln, Yvonna, and Egon Guba, 1985. Naturalistic Inquiry. Thousand Oaks, CA: Sage Publications, Inc.
Rittel, Horst, and Melvin Webber. 1973. “Dilemmas in a General Theory of Planning.” Policy Sciences 4(2): 155-169. doi:10.1007/BF01405730.